KONDENZATOR V IZMENIČNIH TOKOKROGIH

Sestavite vezje, ki je predstavljeno na [@fig:06-AC-R-C.png]. Na levi strni imamo vir napetosti amplitude $\hat{U} = 5 V$ in nanj smo zaporedno priključili upor $R = 2,2 k\Omega$ in kondenzator $C_1 = 1 \mu F$. Preverite napetosti na posameznih elementih.

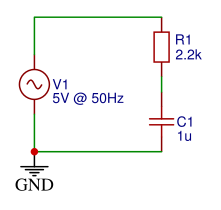Shema priključitve zaporedne vezave upora in kondenzatorja na izmenični vir napetosti.{#fig:06-AC-R-C.png}

NALOGA: NAPETOSTI V IZMENIČNIH TOKOKROGIH

Sestavite vezje na [@fig:06-AC-R-C.png] in z V-metrom izmerite napetosti na elementih in jih vpišite v tabelo. V shemo vključite tudi priključitev vseh treh V-metrov.

| element | $\Tilde{U} [V]$ | |:——-:|—————–| | V1 | | | R1 | | | C1 | | Table: Izmerjene efektivne vrednosti napetosti na elementih v izmeničnem tokokrogu. {#tbl:u-efektivna}

NALOGA: PREVERITE 2. KIRCHHOFFOV IZREK

Kaj lahko ugotovite glede 2. Kirchhoffovega izreka. Ugotovitve zapišite.

Če želimo prikazati časovno odvisnost napetostnega potenciala ($U(t)$) lahko uporabimo merilni inštrument, ki ga imenujemo osciloskop. Priključiti ga moramo tako, kot to prikazuje [@fig:06-OSC.png].

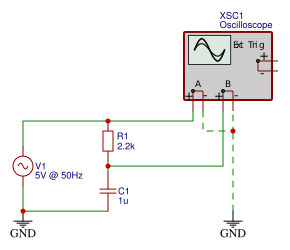Priključitev osciloskopa v vezje.{#fig:06-OSC.png}

NALOGA: ČASOVNI POTEK NAPETOSTI (osciloskop)

V vezje priključite osciloskop, kot kaže [@fig:06-OSC.png].
Nato pravilno nastavite osciloskop (na ekranu naj bo vidna le ena perioda) in odčitajte ter prerišite vse tri poteke napetosti:

  1. Časovni potek napetostnega potenciala, ki ga generira vir napetosti (A).
  2. Časovni potek napetosti na kondenzatorju (B).
  3. Napetost na uporu, ki jo lahko prikažemo z matematično funkcijo A-B.

NALOGA: ČASOVNI POTEK NAPETOSTI (simulacija)

Na isti graf U(t) prikazujte:

  1. Časovni potek napetosti vira,
  2. časovni potek napetosti na kondenzatorju in
  3. časovni potek napetosti na uporu.
    Na graf lahko dodate več krivulj tako, da:
    označite graf -> desni klik -> Properties… -> Traces -> []Show trace X
    Graf naj bo velik, pregleden in na njem naj bo le ena perioda.

Graf čarovne odvisnosti napetosti vira, napetosti na uporu in na kondenzatorju.{#fig:chart-oscilloscope.png}

NALOGA: KARAKTERISTIČNE VREDNOSTI IZMENIČNE NAPATOSTI

Iz predhodno izmerjenega grafa odčitajte naslednje količine in jih vpišite v tabelo. Kjer je:

  • $\hat{U}$ - amplitudna napetost - največji odmik krivulje od srednje vrednosti in
  • $t_{\hat{U}}$ - čas, pri katerem se pojavi amplitudna napetost.
  • $\varphi$ - fazni premik med napetostmi, pri čemer smo za orientacijo vzeli napetost na uporu.1
  • $U_{t=konst.}$ - napetost na elementu ob istem trenutku za vse tri krivulje. Na primer napetost na elementu pri času $t=15ms$.

| element | $\hat{U} [V]$ | $t_{\hat{U}} [ms]$ | $\varphi[^{\circ}]$ | $U_{t=konst.}[V]$ | |:——-:|—————|——————–|:——————-:|——————-| | V1 | | | | | | R1 | | | 0.0 | | | C1 | | | | | Table: Izmerjene karakteristične vrednosti časovnega poteka napetosti. {#tbl:u-t-AC}

Fazni zamik količin v izmeničnih tokokrogih

Za boljšo predstavitev kako lahko razložimo uporabo kazalčnega diagrama (ali faznega diagrama) si odprite primer razlage kosinusne krivulje na enotski krožnici (povezava https://www.geogebra.org/m/cNEtsbvC), ki je prikazan na [@fig:kazalcni-cosinus.png]…

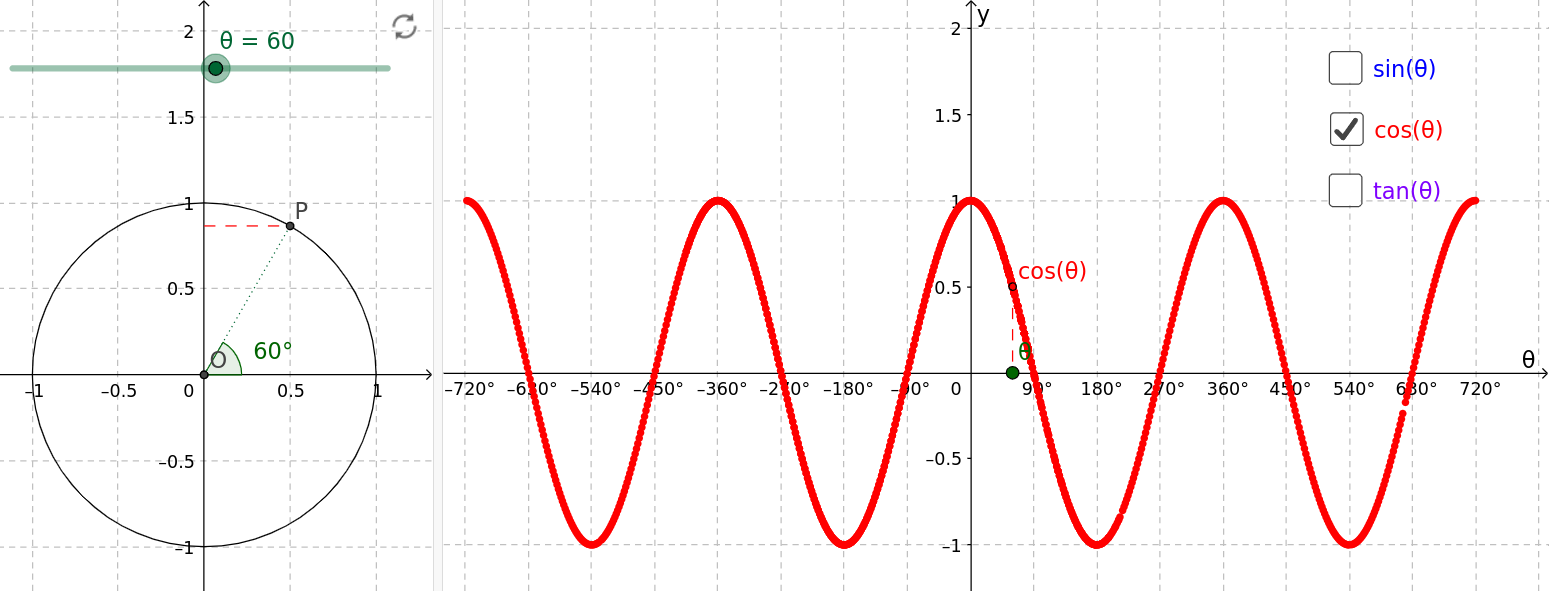Razlaga kosinusne krivulje na enotski krožnici.{#fig:kazalcni-cosinus.png}

… in sledite naslednjim razmislekom:

  1. Zamislite si, da graf na desni strani predstavlja časovni potek napetosti $U(t)$. Enote na $x\ osi$ bi morali zamenjati s časovnimi enotami tako, da bi na mesto $360^{\circ}$ postavili čas ene periode $t_0=20ms$. Enote na $y\ osi$ pa z napetostjo, kjer bi 1 predstavljala največjo napetost = amplitudno napetost $\hat{U}$.
  2. Ta graf na desni strani [@fig:kazalcni-cosinus.png] prikazuje “realne” izmerjene podatke, bodisi z osciloskopom ali pa kot ste jih dobili v grafu v simulaciji.
  3. Graf na levi strani [@fig:kazalcni-cosinus.png] pa prikazuje namišljen matematični prostor, ki nam služi za izračunavanje napetosti in tokov v izmeničnih tokokrogih. Ta prostor je sestavljen iz $Re$ - realne x osi in $Im$ - imaginarne y osi. Le vrednosti na $Re$ osi (rdeča črtkana črta) se odrazijo v realnem svetu in jih je mogoče izmeriti.
  4. V ta prostor vstavimo vektor (kazalec) amplitude napetosti $\vec{\hat{U}}$ in predstavljajte si, da se le-ta vrti v matematični smeri po tem prostoru (kot v animaciji). Ta vektor opravi celoten obhod v času ene periode, kar je v našem primeru $t_0=20ms$, nato se pojav ponavlja.
  5. Torej, na nek način celotnih $\varphi_0=360^{\circ}$ v tem namišljenem prostoru - predstavlja $t_0=20ms$ v realnem svetu.
  6. In prav tako vsakršna poljubna realna časovna razlika $\Delta t$ ustreza faznemu zamiku $\Delta \varphi$ v kazalčnem diagramu.

NALOGA: KAZALČNI DIAGRAM

Najprej preverite 2. Kirchhoffov izrek, vendar vzemite meritve vseh treh napetosti ob istem času iz [@tbl:u-t-AC ]. Kaj ugotovite? Ugotovitev utemeljite v navezavi z meritvami iz [@tbl:u-efektivna ].
V kazalčni diagram vrišite vse tri vektorje amplitudnih napetosti ($\vec{U_{V_1}}, \vec{U_{R_1}} in\ \vec{U_{C_1}}$) in preverite veljavnost 2. Kirchhoffovega izreka še v tej vektorski obliki. Ugotovitev zapišite.

  1. Glej naslednji naslov - FAZNI PREMIK. Fazni premik izračunamo tako, da najprej odčitamo časovno razliko med dvema začetnima točkama dveh krivulj. Tako dobimo $\Delta t$. Nato moramo odčitati še čas dolžine periode ($t_0$), ki je v našem primeru $t_0=20ms$. To je čas, po katerem se fizikalni pojav ponavlja. Če ta čas predstavlja $360^{\circ}$, potem je $\Delta t$ iskani fazni premik $\varphi$. ↩